- General
- Developers
- Mahout-Samsara
- Algorithms
- List of algorithms
- Distributed Matrix Decomposition
- Cholesky QR
- SSVD
- Distributed ALS
- SPCA
- Recommendations
- Recommender Overview
- Intro to cooccurrence-based
recommendations with Spark - Classification
- Spark Naive Bayes
- MapReduce Basics
- List of algorithms
- Overview
- Working with text
- Creating vectors from text
- Collocations
- Dimensionality reduction
- Singular Value Decomposition
- Stochastic SVD
- Topic Models
- Latent Dirichlet Allocation
- Mahout MapReduce
- Classification
- Naive Bayes
- Hidden Markov Models
- Logistic Regression (Single Machine)
- Random Forest
- Classification Examples
- Breiman example
- 20 newsgroups example
- SGD classifier bank marketing
- Wikipedia XML parser and classifier
- Clustering
- k-Means
- Canopy
- Fuzzy k-Means
- Streaming KMeans
- Spectral Clustering
- Clustering Commandline usage
- Options for k-Means
- Options for Canopy
- Options for Fuzzy k-Means
- Clustering Examples
- Synthetic data
- Cluster Post processing
- Cluster Dumper tool
- Cluster visualisation
- Recommendations
- First Timer FAQ
- A user-based recommender
in 5 minutes - Matrix factorization-based
recommenders - Overview
- Intro to item-based recommendations
with Hadoop - Intro to ALS recommendations
with Hadoop
Fuzzy K-Means
Fuzzy K-Means (also called Fuzzy C-Means) is an extension of K-Means , the popular simple clustering technique. While K-Means discovers hard clusters (a point belong to only one cluster), Fuzzy K-Means is a more statistically formalized method and discovers soft clusters where a particular point can belong to more than one cluster with certain probability.
Algorithm
Like K-Means, Fuzzy K-Means works on those objects which can be represented in n-dimensional vector space and a distance measure is defined. The algorithm is similar to k-means.
- Initialize k clusters
- Until converged
- Compute the probability of a point belong to a cluster for every <point,cluster> pair
- Recompute the cluster centers using above probability membership values of points to clusters
Design Implementation
The design is similar to K-Means present in Mahout. It accepts an input file containing vector points. User can either provide the cluster centers as input or can allow canopy algorithm to run and create initial clusters.
Similar to K-Means, the program doesn’t modify the input directories. And for every iteration, the cluster output is stored in a directory cluster-N. The code has set number of reduce tasks equal to number of map tasks. So, those many part-0
Files are created in clusterN directory. The code uses driver/mapper/combiner/reducer as follows:
FuzzyKMeansDriver - This is similar to KMeansDriver. It iterates over input points and cluster points for specified number of iterations or until it is converged.During every iteration i, a new cluster-i directory is created which contains the modified cluster centers obtained during FuzzyKMeans iteration. This will be feeded as input clusters in the next iteration. Once Fuzzy KMeans is run for specified number of iterations or until it is converged, a map task is run to output “the point and the cluster membership to each cluster” pair as final output to a directory named “points”.
FuzzyKMeansMapper - reads the input cluster during its configure() method, then computes cluster membership probability of a point to each cluster.Cluster membership is inversely propotional to the distance. Distance is computed using user supplied distance measure. Output key is encoded clusterId. Output values are ClusterObservations containing observation statistics.
FuzzyKMeansCombiner - receives all key:value pairs from the mapper and produces partial sums of the cluster membership probability times input vectors for each cluster. Output key is: encoded cluster identifier. Output values are ClusterObservations containing observation statistics.
FuzzyKMeansReducer - Multiple reducers receives certain keys and all values associated with those keys. The reducer sums the values to produce a new centroid for the cluster which is output. Output key is: encoded cluster identifier (e.g. “C14”. Output value is: formatted cluster identifier (e.g. “C14”). The reducer encodes unconverged clusters with a ‘Cn’ cluster Id and converged clusters with ‘Vn’ clusterId.
Running Fuzzy k-Means Clustering
The Fuzzy k-Means clustering algorithm may be run using a command-line invocation on FuzzyKMeansDriver.main or by making a Java call to FuzzyKMeansDriver.run().
Invocation using the command line takes the form:
bin/mahout fkmeans \
-i <input vectors directory> \
-c <input clusters directory> \
-o <output working directory> \
-dm <DistanceMeasure> \
-m <fuzziness argument >1> \
-x <maximum number of iterations> \
-k <optional number of initial clusters to sample from input vectors> \
-cd <optional convergence delta. Default is 0.5> \
-ow <overwrite output directory if present>
-cl <run input vector clustering after computing Clusters>
-e <emit vectors to most likely cluster during clustering>
-t <threshold to use for clustering if -e is false>
-xm <execution method: sequential or mapreduce>
Note: if the -k argument is supplied, any clusters in the -c directory will be overwritten and -k random points will be sampled from the input vectors to become the initial cluster centers.
Invocation using Java involves supplying the following arguments:
- input: a file path string to a directory containing the input data set a SequenceFile(WritableComparable, VectorWritable). The sequence file key is not used.
- clustersIn: a file path string to a directory containing the initial clusters, a SequenceFile(key, SoftCluster | Cluster | Canopy). Fuzzy k-Means SoftClusters, k-Means Clusters and Canopy Canopies may be used for the initial clusters.
- output: a file path string to an empty directory which is used for all output from the algorithm.
- measure: the fully-qualified class name of an instance of DistanceMeasure which will be used for the clustering.
- convergence: a double value used to determine if the algorithm has converged (clusters have not moved more than the value in the last iteration)
- max-iterations: the maximum number of iterations to run, independent of the convergence specified
- m: the “fuzzyness” argument, a double > 1. For m equal to 2, this is equivalent to normalising the coefficient linearly to make their sum 1. When m is close to 1, then the cluster center closest to the point is given much more weight than the others, and the algorithm is similar to k-means.
- runClustering: a boolean indicating, if true, that the clustering step is to be executed after clusters have been determined.
- emitMostLikely: a boolean indicating, if true, that the clustering step should only emit the most likely cluster for each clustered point.
- threshold: a double indicating, if emitMostLikely is false, the cluster probability threshold used for emitting multiple clusters for each point. A value of 0 will emit all clusters with their associated probabilities for each vector.
- runSequential: a boolean indicating, if true, that the algorithm is to use the sequential reference implementation running in memory.
After running the algorithm, the output directory will contain:
- clusters-N: directories containing SequenceFiles(Text, SoftCluster) produced by the algorithm for each iteration. The Text key is a cluster identifier string.
- clusteredPoints: (if runClustering enabled) a directory containing SequenceFile(IntWritable, WeightedVectorWritable). The IntWritable key is the clusterId. The WeightedVectorWritable value is a bean containing a double weight and a VectorWritable vector where the weights are computed as 1/(1+distance) where the distance is between the cluster center and the vector using the chosen DistanceMeasure.
Examples
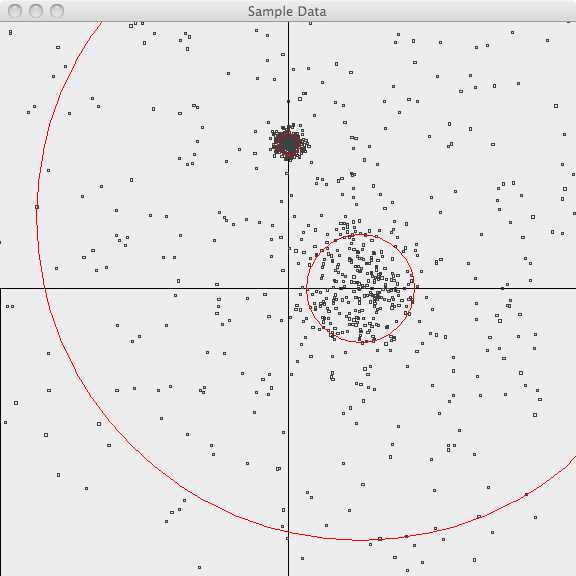
The following images illustrate Fuzzy k-Means clustering applied to a set of randomly-generated 2-d data points. The points are generated using a normal distribution centered at a mean location and with a constant standard deviation. See the README file in the /examples/src/main/java/org/apache/mahout/clustering/display/README.txt for details on running similar examples.
The points are generated as follows:
- 500 samples m=[1.0, 1.0](1.0,-1.0.html) sd=3.0
- 300 samples m=[1.0, 0.0](1.0,-0.0.html) sd=0.5
- 300 samples m=[0.0, 2.0](0.0,-2.0.html) sd=0.1
In the first image, the points are plotted and the 3-sigma boundaries of their generator are superimposed.
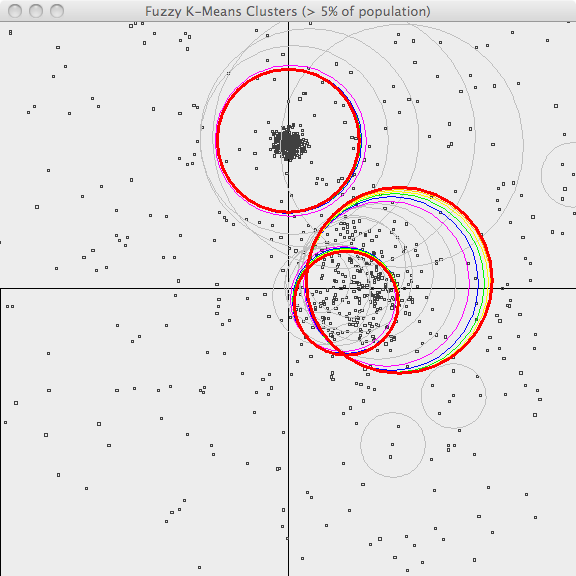
In the second image, the resulting clusters (k=3) are shown superimposed upon the sample data. As Fuzzy k-Means is an iterative algorithm, the centers of the clusters in each recent iteration are shown using different colors. Bold red is the final clustering and previous iterations are shown in [orange, yellow, green, blue, violet and gray](orange,-yellow,-green,-blue,-violet-and-gray.html) . Although it misses a lot of the points and cannot capture the original, superimposed cluster centers, it does a decent job of clustering this data.
The third image shows the results of running Fuzzy k-Means on a different data set which is generated using asymmetrical standard deviations. Fuzzy k-Means does a fair job handling this data set as well.

